ユーザーの行動履歴から、その興味に応じたアイテムを推薦したいとき、最も魅力的な手法の一つに行列分解があります。中でも、 iALS (implicit Alternating Least Squareの略) と呼ばれるモデルは、スケーラブルでかつ精度面でも強力な、ほとんど唯一のモデルです。

ところが、iALSの効率のよい解法や、チューニングを正しく行った上での精度は、（特に日本語文献で）あまり知られていません。本記事は、iALSの真の実力とそのような現状とのギャップを埋めるためのものです。

1. はじめに

こんにちは。株式会社ビズリーチのAIグループでデータサイエンティストをしている大槻と申します。

我々AIグループのミッションは、Visionalグループ各社・各事業にデータを活用したイノベーションを提供することです。技術ドリブンではなく課題ドリブンで事業に貢献する、という指針のもと、直近半年だけで21個の新規機能開発・精度改善を本番環境で実現しており、事業貢献の質・量ともに充実していると自負しております。この度、これまでの貢献が認められ、（手前味噌ですが）AIグループを代表して、株式会社ビズリーチで半期に一度行われるキックオフにて、最高技術賞という栄えある賞をいただきました。

本記事では、受賞記念（？）として、著者が日頃の業務に愛用しているimplicit Alternating Least Square (iALS) という推薦モデルについて語りたいと思います。この題材を特に選んだ理由は、iALSは古典的 (原論文は2008年) かつポピュラーな手法であるにも関わらず、その真価が広くは知られていないと思ったからです。本記事では、以下のようなことを伝えられれば、と思います。

2. 問題設定とiALS損失関数の定義

2.1. 入力データ（暗黙的フィードバック）

今回扱う学習データは、全て暗黙的フィードバック (implicit feedback) であるとします。すなわち、学習の元データは下の表に示すような「どのユーザーが、どのアイテムと接触した」という二列のテーブルです。

user_id item_id
1 11
1 12
2 12
2 13
2 14
3 11
3 13

以下では、この表データは $X$ という行列にまとめられているとします。上記テーブルに含まれる user_id 数を $N_U$ , item_id 数を $N_I$ とするとき、 $X$ は $ N_U \times N_I$ 行列であり、その第 $i$ 行は user_id として $\mathrm{user}[i]$ を持つユーザーに、第 $j$ 列 は item_id として $\mathrm{item}[j]$ を持つアイテムに対応するとします。このマッピングのもと、 $X$ の $i$ 行 $j$ 列の要素は、以下の式で与えられます。

$$ X_{ij} = \begin{cases} 1 & (\text{if } \mathrm{user}[i] \text{ and } \mathrm{item}[j] \text{ had contact})\\ 0 & (\text{otherwise}) \end{cases} $$

すなわち、$\mathrm{user}[i]$ と $\mathrm{item}[j]$ の組み合わせが、上記のテーブルに存在すればその要素は1,　そうでなければ0ということです。

たとえば、上の例の小さなテーブルに対しては、 $N_U=3$、$N_I=4$ で、$X$ は以下のようになります。

$$ X = \left( \begin{array}{cccc} \ 1\ & \ 1\ & \ 0 \ & \ 0\ \\ \ 0\ & \ 1\ & \ 1 \ & \ 1\ \\ \ 1\ & \ 0\ & \ 1 \ & \ 0
\end{array} \right) $$

この場合、$X$ の行・列とuser/item IDのマッピングは以下の配列で与えられます。

\begin{align*} \mathrm{user} &= [1, 2, 3] \\ \mathrm{item} &= [11, 12, 13, 14] \end{align*}

2.2. 行列分解による推薦アルゴリズム

行列分解では、$X$の第 $i$ 行に対して、そのユーザーの「嗜好」を表す $d$ 次元ベクトル $ \mathbf{u}_i $ が存在すると仮定します。また、 $X$の第 $j$ 列に対しては、対応するアイテムの「特性」を表す、やはり $d$ 次元のベクトル $\mathbf{v}_j$ が存在するとします。

これらのベクトルが求められた時、ユーザー $i$ が アイテム $j$ を好む度合いは内積

$$ \mathbf{u}_i \cdot \mathbf{v}_j $$

で表されると考えます。文字通り「興味のベクトルが揃う」とき、ユーザー $i$ のアイテム $j$ に対するスコア値 $ \mathbf{u}_i \cdot \mathbf{v}_j $ は大きくなります。

2.3. SVDの損失関数

一口に行列分解といってもさまざまなモデルがあるのですが、ここではストレートに $\mathbf{u}_i \cdot \mathbf{v}_j$ が $X_{ij}$ に近くなるように、以下のような損失関数を考えます。この損失関数に対する最適解は、実はよく知られたアルゴリズムである特異値分解 (SVD) によって得ることができるので、「SVDの損失関数」といえます。

\begin{align} L^{(\text{SVD})} &= \frac{1}{2} \sum_{i=1}^{N_U} \sum_{j=1}^{N_I} (\mathbf{u}_i \cdot \mathbf{v}_j - X_{ij})^2 = \frac{1}{2} \left[ \sum _{ (i, j) \in S} ( \mathbf{u}_{i} \cdot \mathbf{v}_j - 1)^2 + \sum_{\substack{1 \le i \le N_U \\ 1 \le j \le N_I \\ (i, j) \notin S} } ( \mathbf{u}_{i} \cdot \mathbf{v}_j - 0)^2 \right] \label{eq:svdLoss} \end{align}

ここで、$S$ は $X_{ij} = 1 $ となる $(i, j)$ の組み合わせ全体を指します:

\begin{align} S = \left\{ (i, j) \, | \, X_{ij} = 1 \right\} \label{eq:S} \end{align}

これにより、接触がある $X_{ij} = 1$ の組み合わせに対しては $\mathbf{u}_{i}\cdot \mathbf{v}_j$ は1に近く、そうでない組み合わせに対しては0に近くなるような $\mathbf{u}$, $\mathbf{v}$ が選択されるはずです。

2.4. iALSの損失関数

SVDの損失関数 \eqref{eq:svdLoss} では、 $X_{ij} = 1$ の場合も、 $X_{ij} = 0$ の場合も、予測値 $ \mathbf{u}_i \cdot \mathbf{v}_{j}$ が $X_{ij}$ から外れた場合のペナルティは同じに設定されています。 iALSでは、以下のような動機から、前者と後者に別の重みでペナルティを課します:

iALSの損失関数は、\eqref{eq:svdLoss} に以上の考察を取り込んだものです:

$$ L = \frac{1}{2} \left[ (1 + \alpha_0 ) \sum_{ (i,j) \in S } ( \mathbf{u}_i \cdot \mathbf{v}_j - 1 ) ^ 2 + \alpha_0 \sum_{\substack{1 \le i \le N_U \\ 1 \le j \le N_I \\ (i, j) \notin S} }( \mathbf{u}_i \cdot \mathbf{v}_j - 0 ) ^ 2 \right] $$

ここで、 $\alpha_0 > 0$ は新たなハイパーパラメータになります。この導入により、 $X_{ij} = 1$ となる $(i,j)$ に対して $\mathbf{u}_i \cdot\mathbf{v}_j$を1に近づける方が、$X_{ij} = 0 $ の箇所の予測値を 0 に近づけるよりも $(1 + \alpha _ 0 ) / \alpha_0$ 倍だけ得になります。

最後に正則化項を導入して、損失関数 $L^{(\mathrm{iALS})}$ の完成です。新たに導入されたハイパーパラメータ $\lambda$ は正則化係数と呼ばれます。

\begin{align} L^{(\mathrm{iALS})} & = \frac{1}{2} \left[ (1 + \alpha_0 ) \sum_{(i,j) \in S } ( \mathbf{u}_i \cdot \mathbf{v}_j - 1 ) ^ 2 + \alpha_0 \sum_{\substack{1 \le i \le N_U \\ 1 \le j \le N_I \\ (i, j) \notin S} }( \mathbf{u}_i \cdot \mathbf{v}_j - 0 ) ^ 2 \right] \nonumber \\ &+ \frac{\lambda}{2} \left[ \sum_{1 \le i \le N_U } || \mathbf{u}_i || ^2 + \sum_{1 \le j \le N_I } || \mathbf{v}_j || ^2 \right] \label{eq:ialsLoss} \end{align}

なお、原論文では $\alpha_0$ の代わりに $ \alpha = 1 / \alpha_0 $というパラメータを用いていており、正則化係数についても違った規格化を採用しています ($ \lambda = \lambda^{(\text{原論文})} * \alpha_0 $)。

3. iALS損失関数の最小化

ここでは、損失関数 \eqref{eq:ialsLoss} の最適化手法である暗黙的交代最小二乗法 (implicit Alternating Least Square) について述べます。 iALSというのは本来最小化の手法の名前であって、モデルを表すものではないのですが、鮮やかな手法なのでモデル自体の名前として広く使われるようになったようです。

損失関数 \eqref{eq:ialsLoss} には、 $ (\mathbf{u}_1 \cdot \mathbf{v}_1) ^ 2 $ のような、未知パラメータについて4次の項が含まれており、このことが最小化を複雑にしています。しかし、 $\mathbf{v}$ を固定すれば損失関数は $\mathbf{u}$ について二次式であり、厳密な最小化が可能になります。 そこで、 iALSでは以下の手続きにより損失関数の最小化を試みます。

  1. ($U$-step) $ \left\{ \mathbf{v}_j \right\} _{j=1} ^ {N_I} $ 全てを固定して $ \left\{ \mathbf{u}_i \right\} _{i=1} ^ {N_U} $について $L^{(\mathrm{iALS})}$の 最小化を行う。
  2. ($V$-step) $ \left\{ \mathbf{u}_i \right\} _{i=1} ^ {N_U} $ 全てを固定して $ \left\{ \mathbf{v}_j \right\} _{j=1} ^ {N_I} $について $L^{(\mathrm{iALS})}$の 最小化を行う。
  3. 収束基準に達すれば終了。達していなければ1. に戻る。

$U$-step・$V$-stepの両方で、必ず損失関数の値は減少するため、十分なエポック数の繰り返しによって極小値に近づけることが期待されます。多くの場合、数十エポックほど $U$-stepと $V$-stepを交互に繰り返せば、満足のいく解が得られます。

続いて、 $U$-stepの中身について細かく検討していきます。まずは、 $ L^{(\mathrm{iALS})} $ をユーザー $i$ にのみ関連する項 $L_{i}$ に分解します。

\begin{align} L^{(\mathrm{iALS})} & = \sum_{i=1} ^{N_U } L_{i} + ( \left\{ \mathbf{u}_i \right\}_{i=1} ^{N_U } \text{に依存しない項}) \end{align}

ここで、 $L_{i}$ は以下の式で定義されます。

\begin{align} L_i & = \frac{(1 +\alpha _0)}{2}\sum_{j \in U(i)} (\mathbf{u}_i \cdot \mathbf{v}_j - 1 ) ^ 2 + \frac{\alpha _0}{2}\sum_{j \notin U(i)} (\mathbf{u}_i \cdot \mathbf{v}_j ) ^ 2 + \frac{\lambda}{2} || \mathbf{u}_i || ^ 2 \label{eq:Li} \end{align}

ただし、 $U(i)$ は非零添字集合 $S$ \eqref{eq:S} を $i$ についてスライスしたもので、以下のように定義されます。 \begin{align} U(i) := \left\{ j \ | \ X_{ij} = 1 \right\} \end{align}

\eqref{eq:Li} をもっと整理して、 $\mathbf{u}_i$ について二次の項と一次の項を取り出し、

\begin{align} L_{i} = \frac{1}{2} \mathbf{u}_i ^T P _i \mathbf{u}_i - \mathbf{q}_i ^T \mathbf{u}_i + 定数 \end{align}

という形に持っていきましょう。ここで、 $P_i$ は $d\times d$ 行列、 $\mathbf{q}_i$ は $d$ 次元ベクトルになります。

まず、 $L_{i}$ の $\mathbf{u}_i$ について二次の部分 $L_i ^{(2)}$ は以下のように書けます:

\begin{align*} L_i^{(2)} = & \frac{1 + \alpha _0 }{2}\sum_{j \in U(i)} \mathbf{u}_i ^T \mathbf{v}_j \mathbf{v}_j ^T \mathbf{u}_i + \frac{\alpha _0 }{2}\sum_{j \notin U(i)} \mathbf{u}_i ^T \mathbf{v}_j \mathbf{v}_j ^T \mathbf{u}_i + \frac{\lambda}{2} \mathbf{u}_i ^T \mathbf{u}_i \\ =& \frac{1 }{2}\sum_{j \in U(i)} \mathbf{u}_i ^T \mathbf{v}_j \mathbf{v}_j ^T \mathbf{u}_i + \frac{\alpha_0}{2} \sum_{j=1}^{N_I} \mathbf{u}_i ^T \mathbf{v}_j \mathbf{v}_j ^T \mathbf{u}_i + \frac{\lambda}{2} \mathbf{u}_i ^T \mathbf{u}_i \end{align*}

$\mathbf{u}_i$をくくり出して、 $\frac{1}{2} \mathbf{u}_i ^T P _i \mathbf{u}_i $ の形に持っていくと、 \begin{align} P_{i} = \sum_{j \in U(i)} \mathbf{v}_j \mathbf{v}_j ^T + \alpha_0 \sum_{j=1}^{N_I} \mathbf{v}_j \mathbf{v}_j ^T + \lambda E _d \label{eq:Pi} \end{align}

がわかります。 $E_d$ は $d$ 次元の単位行列です。

続いて $L_i$ の$\mathbf{u}_i $ について一次の項 $L_i ^{(1)} $ を取り出します。これは \eqref{eq:Li} の第一項 $ \frac{(1 +\alpha _0)}{2}\sum_{j \in U(i)} (\mathbf{u}_i \cdot \mathbf{v}_j - 1 ) ^ 2 $ のみから生じ、以下のようになります:

\begin{align*} L^{(1)}_i = - (1 + \alpha _0 )\sum_{j \in U(i)} \mathbf{v}_j ^ T \mathbf{u}_i \end{align*}

よって $\mathbf{q}_i$ の形は以下になることがわかります。

\begin{align} \mathbf{q}_i = (1 + \alpha _0 )\sum_{j \in U(i)} \mathbf{v}_j \end{align}

まとめると、$U$-stepは、ユーザー $i$ ごとに以下の部分問題を解くことに帰着されます:

\begin{align} & \mathbf{u}_{i} = \mathrm{arg}\min_{\mathbf{u}\in \mathbb{R}^d} \left(\frac{1}{2} \mathbf{u} ^T P _i \mathbf{u} - \mathbf{q}_i ^T \mathbf{u}\right) \nonumber \\ \text{where} \quad & \nonumber \\ & P_{i} = \sum_{j \in U(i)} \mathbf{v}_j \mathbf{v}_j ^T + \alpha_0 \sum_{j=1}^{N_I} \mathbf{v}_j \mathbf{v}_j ^T + \lambda E _d \nonumber \\ & \mathbf{q}_i = (1 + \alpha _0 )\sum_{j \in U(i)} \mathbf{v}_j \label{eq:subProblem} \end{align}

ここで二つ重要なポイントを挙げます。

$ \left\{ \mathbf{v}_i \right\} _{i=1} ^{N_I }$ についての最適化ステップである $V$-stepについても同様に問題を分解することができます。本節の残りでは、部分問題 \eqref{eq:subProblem} の解き方について詳述していきたいと思います。

3.1. コレスキー分解による厳密解法

原論文での解法では、特に細工はせずに$P_i$, $\mathbf{q}_i$を計算し、厳密に \eqref{eq:subProblem} を解くことを試みます。 $ \frac{1}{2} \mathbf{u} ^T P _i \mathbf{u} - \mathbf{q}_i ^T \mathbf{u}$ を $\mathbf{u}$で微分して係数を0とおくと、

\begin{align} P_i \mathbf{u} - \mathbf{q}_i = 0 \end{align}

なので、 $P_i$ の逆行列でもって

\begin{align} \mathbf{u} = P_i ^{-1}\mathbf{q}_i \end{align}

が得られます。この手法で要する計算量について検討すると、

ここで、 $|U(i)|$ は $U(i)$ の要素数を意味し、 $\sum_i |U(i)| = |S|$ が成り立ちます。 $V$-stepでの計算量も同様であることに注意すると、1エポック全体での計算量は以下で与えられることがわかります:

\begin{align} O(|S| d^2 + (N_U + N_I) d^3) \end{align}

ただし、計算のほとんどの部分は並列化が可能であり、プロセッサが多いマシンでは大幅な高速化が期待されることに注意しましょう。

この方法の実装は簡単で、多くのライブラリに実装されています。しかし、いくら並列化効率が高いとはいえ、$O(d^3)$ の負担は大きく、現実的なデータセットで大きな次元 $d$ のモデルを学習するのには大変な時間を要します。また、 $|S|$ 、すなわち $X_{ij}$ の非零要素数が大きいと、 $P_i$ の計算に由来する部分 $ O(|S| d^2) $ も厳しくなります。

近似解法ではあるものの、 $d$ の増加に伴う計算量の増大を緩和してくれるのが、著者イチオシの共役勾配法になります。

3.2. 共役勾配法による近似解法

“Applications of the conjugate gradient method for implicit feedback collaborative filtering”は、共役勾配法という反復による最適化手法を \eqref{eq:subProblem} の最小化に応用すれば、精度をおおむね保ちながらも大幅な高速化が可能だ、という論文です。共役勾配法の詳細については触れることができないので、詳細は 有名なチュートリアル を参照していただければ、と思います。

共役勾配法の利点をかいつまんで述べますと、

  1. $P_i$ の具体的な形を知らなくても、任意のベクトル $\mathbf{x}$ について $P_i \, \mathbf{x}$ が計算できれば十分である
  2. $P_i$ によるベクトル積演算を高々 $d$ 回行うと厳密解が得られる。 また、 $d$ 回 $P_i$ の掛け算をせず、一定の反復回数 $C$ で打ち止めにしたとしても、十分よい近似になっていることが多い

そこで、共役勾配法による $U$-stepの計算量は以下のようになります。

コレスキー分解の際に必要だった $P_i$ の計算が不要なことに注意しましょう。その代わり、 $P_i$ によるベクトル積演算のコストが $O(Cd^2)$ でなくて、 $O(C (d^2 + |U(i)|d ))$ になっています。これらは以下のように $P_i \, \mathbf{x}$ を計算するからです:

\begin{align*} P_i \, \mathbf{x} & = ( \Pi + \sum_{j\in U(i)}\mathbf{v} \mathbf{v}_i ^T + \lambda E_d) \mathbf{x} \\ & = \Pi \, \mathbf{x} + \sum _{j\in U(i)} (\mathbf{v}_j \cdot \mathbf{x}) \mathbf{v}_j + \lambda \mathbf{x} \end{align*}

$\Pi \, \mathbf{x}$ は $O(d^2)$, 内積 $\mathbf{v}_j \cdot \mathbf{x} $ は $O(d)$, スカラー・ベクトル積 $(\mathbf{v}_j \cdot \mathbf{x}) \mathbf{v}_j$ も $O(d)$ であることに注意しましょう。

$V$-stepの計算量についても同様です。 結果、1エポックのトータルでの計算量は

\begin{align} O( C|S| d + C (N_U + N_I) d^2) \end{align}

で、コレスキー分解の時と比べて $d$ が一つ減っていることがわかります。 $C$の値については、多くの場合 $C=3$ で十分です。これには、2エポック目以降は直前のエポックでの $U$-stepの結果を共役勾配法の反復の初期点とすれば、最初から解に近いところでスタートできる、という工夫も効いています。

共役勾配法によるiALSの解法は、その速度にもかかわらず広くは知られていないようで、学術論文でもこの貢献が無視されることがあるのは残念に思います。共役勾配法を実装したライブラリには、たとえば implicit や、手前味噌ですが著者が実装した irspack が存在します（ Eigenを使っているおかげでimplicitより速いはずです、是非お試しください）。

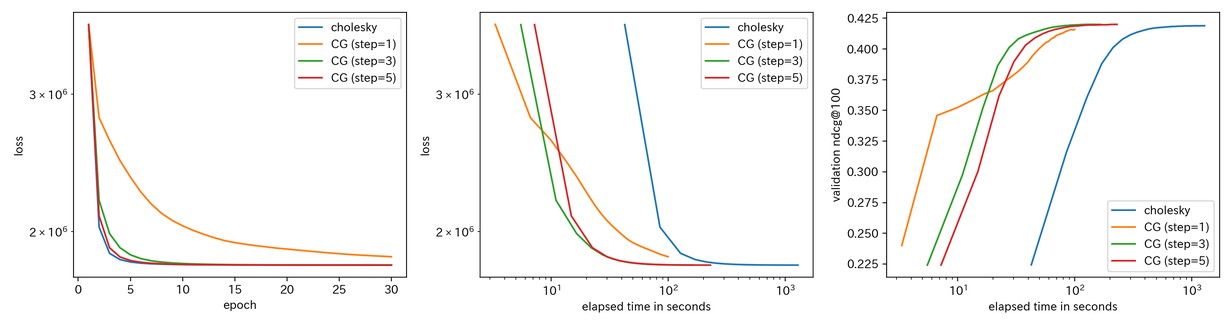
コレスキー分解と共役勾配法の速度・精度比較

コレスキー分解と共役勾配法の差異を理解するため、ここではMovielens 20Mデータを用いた実験を行います。データの前処理・分割については、頻繁に用いられる Mult-VAEのプロトコル に従います。モデルのパラメータについては、ある程度チューニング済みの値である

を用いました。

下図に、

  1. エポック数と損失関数の値の関係
  2. 計算の経過時間と損失関数の値の関係
  3. 計算の経過時間と検証データに対するNDCG@100の値の関係

をアルゴリズムごとにプロットしたものを示します。共役勾配法 (下図ではCGとラベルされています)については、ステップ数 $C$ を1, 3, 5と変化させました。

コレスキー分解と共役勾配法の速度・精度比較
エポック数・計算時間に対する損失関数と validation NDCG@100 の関係

エポックごとの損失関数の減り具合という点ではやはりコレスキー分解が一番収束しやすいのですが、計算時間ベースでは共役勾配法が圧倒的に有利である様子が見て取れると思います。

3.3. 部分空間に注目した逐次解法

最後に、近年登場した手法である eALS (element-wise Alternating Least Square)と、その一般化である iALS++ という手法について簡単に触れたいと思います。

eALSは座標降下法（coordinate descent）というよく知られた手法を \eqref{eq:subProblem} に適用したもので、二次形式

\begin{align*} f(\mathbf{u}) := \frac{1}{2} \mathbf{u} ^T P \mathbf{u} - \mathbf{q} ^T \mathbf{u} \end{align*}

の最小化問題を、以下のように各々の座標成分ごとの一変数問題に帰着させます。

但し、$u_a$ はベクトル $\mathbf{u}$ の第 $a$ 成分を表します。eALSでは、巧妙にキャッシュを用いることで、1エポックの計算量を

$$ O( |S| d + (N_U + N_I) d^2) $$

まで落とすことができます。これは共役勾配法と同程度の計算量になっています。ただ、 iALS++ 論文においては、この方法はベクトル化演算が使えず、モダンなCPUの性能をフルに活かすことができないと指摘されています。

iALS++は、eALSの欠点(ベクトル化演算が使えないこと)を補うため、座標をひとつずつ最適化するのではなく、いくつかのブロックにまとめて最適化することを提案しています。たとえば、ブロックの大きさ $B = 4$ の時は、

という手続きを行います。これによって理論上の計算量は、以下のようにeALSより上がってしまいます:

$$ O((N_U + N_I)(d^2 + B^2 d) + B |S| d) $$

ところが、座標ブロックに分割された各々の問題はそれぞれがベクトル化演算により効率よく解ける形になるため、実用的な問題ではeALSよりもiALS++の方が速いし、エポック単位で見ても収束が速いことが報告されています。

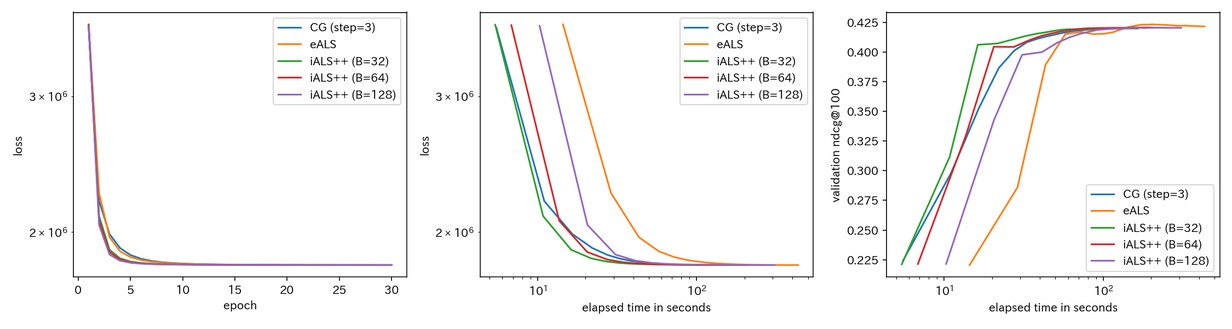
共役勾配法vs eALS vs iALS++ の速度・精度比較

コレスキー分解vs共役勾配法と同様の状況設定で、 eALSとiALS++ の速度・精度比較を行いました。iALS++ ついてはブロックの大きさ $B$ を32, 64, 128と変化させています。

共役勾配法と部分空間ベースの方法の速度・精度比較
eALS・iALS++ におけるエポック数・計算時間に対する損失関数と validation NDCG@100 の関係

が結論かと思います。

4. 精度面での最近の進展

本節では、最近の成果として、iALS++と同時に同じ著者陣によって投稿された論文 “Revisiting the Performance of iALS on Item Recommendation Benchmarks” による精度改善について簡単に説明したいと思います。

この論文のキモは、 iALSの損失関数 \eqref{eq:ialsLoss} の正則化項を以下のように変更した上でチューニングを行うことで、Movielens 20Mなどのベンチマークデータに対して大幅な精度向上が得られる、というものです:

\begin{align} L^{(\mathrm{iALS++})} & = \frac{1}{2} \left[ (1 + \alpha_0 ) \sum_{(i,j) \in S } ( \mathbf{u}_i \cdot \mathbf{v}_j - 1 ) ^ 2 + \alpha_0 \sum_{\substack{1 \le i \le N_U \\ 1 \le j \le N_I } }( \mathbf{u}_i \cdot \mathbf{v}_j - 0 ) ^ 2 \right] \nonumber \\ &+ \frac{\lambda}{2} \left[ \sum_{1 \le i \le N_U } (\alpha _0 N_I + |U(i)|) \, || \mathbf{u}_i || ^2 + \sum_{1 \le j \le N_I } (\alpha _0 N_U + |I(j)| ) \, ||\mathbf{v}_j || ^2 \right] \end{align}

ここで、 $I(j)$ は非零要素集合 $S$ のアイテム $j$ についての集合です: \begin{align} I(j) := \left\{ i \ | \ X_{ij} = 1 \right\} \end{align} つまり、出現頻度の高いユーザーほど $ (\alpha _0 N_I + |U(i)|) $ によって強く正則化を行うべし (frequency-based regularization) という主張です。この動機について論文には以下のように述べられています:

  1. レーティング予測など、明示的フィードバックデータを用いる際は、出現頻度の高いユーザー/アイテムほど強い正則化係数が課される方が、精度が向上することが知られている
  2. iALSも $X_{ij} = 1 \text{ or } 0$ を予測するレーティング問題だと思って、同じことをする。
    • そのとき、ユーザー $i$ に対する正例の個数は $U(i)$ 個、負例の個数は $N_I - | U(i) | \simeq N_I $個である
    • ただし、負例の重みは正例に比べて約$\alpha_0$倍なので、ユーザーの正味の登場数は $ \alpha _0 N_I + |U(i)| $と思う

個人的には、以下の雑な議論の方が $ (\alpha _0 N_I + |U(i)|) $ という因子の出どころとしては納得がいくように思いました:

すなわち、正則化項に $ (\alpha_0 N_I + |U(i)|)$ というファクターを導入すると、 $N_U$, $N_I$, $\alpha_0 $ の値によらず、$P_i$ の第二項までの固有値と正則化項の振幅比は自然に $\lambda$ 程度になります。よって、どのような問題でも $\lambda$ に対する探索は常に同じような範囲 (論文では $[0.0003, 1]$ が推奨されています) で行っていれば最適な値が見つけられる、と考えられます。実際、この論文で報告されているパラメータでは、正則化係数の実効値$ \lambda (\alpha_0 N_I + |U(i)|) $ は従来の $\lambda$ より遥かに大きくなります。例えば、Movielens 20Mに対して、従来のモデルのチューニングで得られるパラメータの一例は

です（近年の網羅的なサーベイより）。一方、この論文で報告されているパラメータは

となっています。$\alpha_0$ のスケールは変わらないものの、次元 $d$ が大幅に増え、また正則化係数の実効値も遥かに大きくなっていることがわかります。どうやら、Movielens 20Mにおいては、従来の $\lambda$ の探索範囲が $P_i$ 第二項までのスケールと比べて圧倒的に小さく、$\lambda$ がほぼ効いていなかった、という事情があるようです。著者が実験したところ、frequency-based scalingを用いずとも、従来のモデル定義のままで大きめのレンジで正則化係数を探索すれば、論文と同様の高い精度が得られることがわかりました。

何はともあれ、論文ではMovielens 20MやMillion Songs Datasetなどの大規模データセットについて、従来報告されていたiALSの精度からの大幅な改善が報告されています。深層学習ベースの手法や Embarrassingly Shallow Auto-Encoder ($\mathrm{EASE}^R$) など、最先端の手法でも、一貫してiALSを上回るモデルは存在しないようです。

5. まとめ　

長くなってしまいましたが、この記事ではiALSを用いた行列分解モデルとその解法、そして精度面について最近なされた重要な指摘について述べてきました。特に、共役勾配法とiALSの相性が非常によいことを伝えられていれば幸いです(このことを指摘した論文の引用数が比較的少ないことに義憤を感じていました)。

行列分解というくくりでは、iALSよりも Bayesian Personalized Ranking (BPR) + SGDを適用した結果の方を頻繁に見かける気がします。しかし、最近のサーベイや著者の個人的な経験によれば、BPRやその派生形がiALSに勝てる事例はほとんどなさそうに思います。もしBPRなどを用いているのであれば、一度iALSを4節で触れた論文に従ってチューニングしてみると精度改善が得られるかもしれません。

dimensional_homegoer(異次元の帰宅者)
dimensional_homegoer(異次元の帰宅者)

株式会社ビズリーチ AIグループ データサイエンティスト。割と数値計算なら何でも好きです。在宅勤務が長引き、自分のアイデンティティを見つめ直す日々です。