今回は、AIグループの研究の一環として、転職サービス界隈で徐々に浸透してきている年収推定サービスを参考に、ビズリーチ(サービス)のデータを使って、会員様のレジュメから年収を推定する というテーマに取り組んだ話をします!(2020年8月現在、社内でPOC実施中)
※AIグループは、AIを活用した将来のプロダクト開発に向けて、様々な研究テーマに取り組む社内の研究開発機関です。
※この取り組みは、短期的な実用化を目指したものではなく、研究開発という位置づけで行っているものです。
この一連の取り組みとアイディアをまとめた研究内容がKDD2020併設ワークショップ “Talent and Management Computing 2020” に採択されましたので、詳細についてはそちらもご覧ください。
年収推定三つの壁
学会とかに行って「年収推定って難しくない?できるもんなんすかね?」と同業他社の複数の人に声をかけられたことがあります。自分でやってみても思ったんですが、確かに年収推定は難しいです。。普通の機械学習における回帰問題として解こうとする場合には以下の困難が(少なくともビズリーチのデータには)ありました:
-
そもそも正確 & 多量のデータを集めるのが難しい。
当たり前ですが、年収はとても繊細な個人情報で、そもそもデータを持っている企業は限られていると思います。転職サービスという性質上、ビズリーチでは登録時に必須情報として年収の入力をお願いしています。ただ、匿名化の一貫として、正確な値ではなく「750万円〜1000万円」のような区分値の入力をお願いしており、下の表のように示すように、これは結構粗い離散化になっています。この時点で、回帰問題としての定式化にはなんらかの工夫が必要なことがお分かりいただけると思います。 -
レジュメから見えない要素(ノイズ)の存在
年収がレジュメに書いてある情報だけから決まる訳はないですよね。レジュメだけでその人の全てがわかるのであれば、そもそも面接は要らないことになってしまいますし。レジュメからは見えない情報(ノイズ)の効果はこのくらいあるだろう、ということについても正しく見積もらないと、予測は全く信頼ができないものになってしまいます。 -
年収分布の非正規性
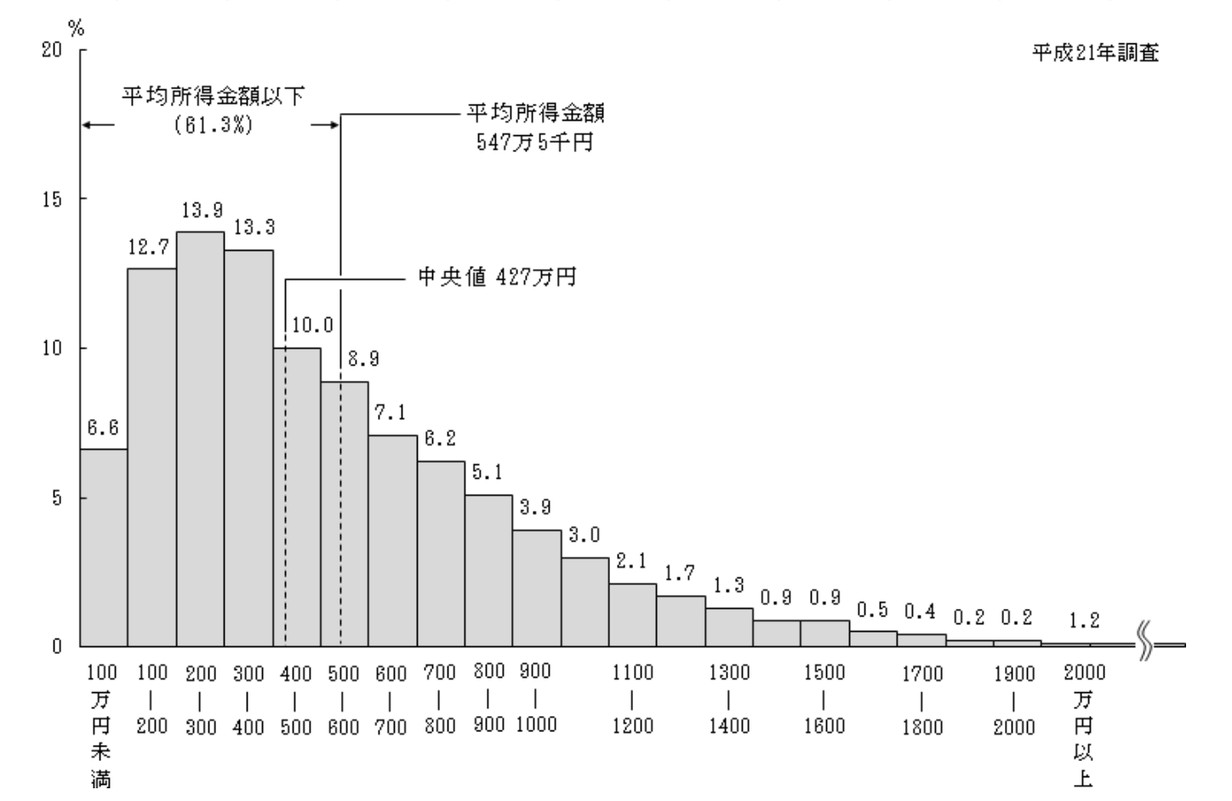
「年収分布では平均値と中央値に大きな隔たりがある」とはよく言われます(下図参照)。また、非正規性は上で述べたノイズの問題とも密接に関わっておりまして、例えば「年収300万円のところ、500万円と誤予測してしまう」のと「年収1000万円のところ、1200万円と誤予測してしまう」のとでは、惜しさが全く違うのは直感的に正しいと思います。年収の真の分布は低レンジで対数正規分布、高レンジでパレート分布に従う、という経験則が知られています(たとえばこの文献の議論を参照)ので、とりあえずは対数をとれば一旦この問題は回避できそうにも思えますが、ビズリーチはハイクラス向けサービスであり、対数正規性が早々に破綻するかも分かりません。
| index | 下限(万円) | 上限(万円) |
|---|---|---|
| 0 | N/A | 500 |
| 1 | 500 | 600 |
| 2 | 600 | 750 |
| 3 | 750 | 1000 |
| 4 | 1000 | 1250 |
| 5 | 1250 | 1500 |
| 6 | 1500 | 2000 |
| 7 | 2000 | 3000 |
| 8 | 3000 | 5000 |
| 9 | 5000 | $\infty$ |
今回の論文では、これらの3点全てに対処するアプローチとして、問題を順序回帰として定式化 + 補間曲線を用いて連続値を回復というアプローチを提案しました。
順序回帰による定式化
以下では、レジュメ情報は$X$という形でスパースな$D$次元のベクトルにまとめられており、それらから$K$(今回は$K=10$)クラスの年収区分値$c$を推定する、という問題を考えます。まずは問題を順序ロジット/順序プロビット回帰として定式化します。若干マイナーなテクニックなのでおさらいをしたいと思います。
冒頭で申し上げた通り、ビズリーチの年収データは「750万円〜1000万円」とか「1000万円〜1250万円」のよう区分値コードになっております。もちろんレジュメ情報からこれらのカテゴリを予測する多クラス分類問題としても定式化を行うことはできますが、それでは区分値間の近さ(誤分類した時の惜しさ)という情報は抜け落ちてしまいます。順序回帰はこういった「クラス間に順序がある場合の分類問題」に対する自然な定式化を与えてくれます。
まず、レジュメ情報$X$を変数とし$\mathcal{W}$をパラメータ集合とするなんらかの(例えば$X$について線形な)関数 $f(X; \mathcal{W})$と、ノイズ分布 $\mathcal{R}$ の存在を仮定し、
$$ \varepsilon \sim \mathcal{R} \\ z = f(X; \mathcal{W}) + \varepsilon $$
という量 $z$ を考えます。$f(X;\mathcal{W}) $ は「レジュメから期待される給与スコア」的なもの、$\varepsilon$は冒頭でも述べた、「レジュメからは見えない要因」を表す確率変数と思います。
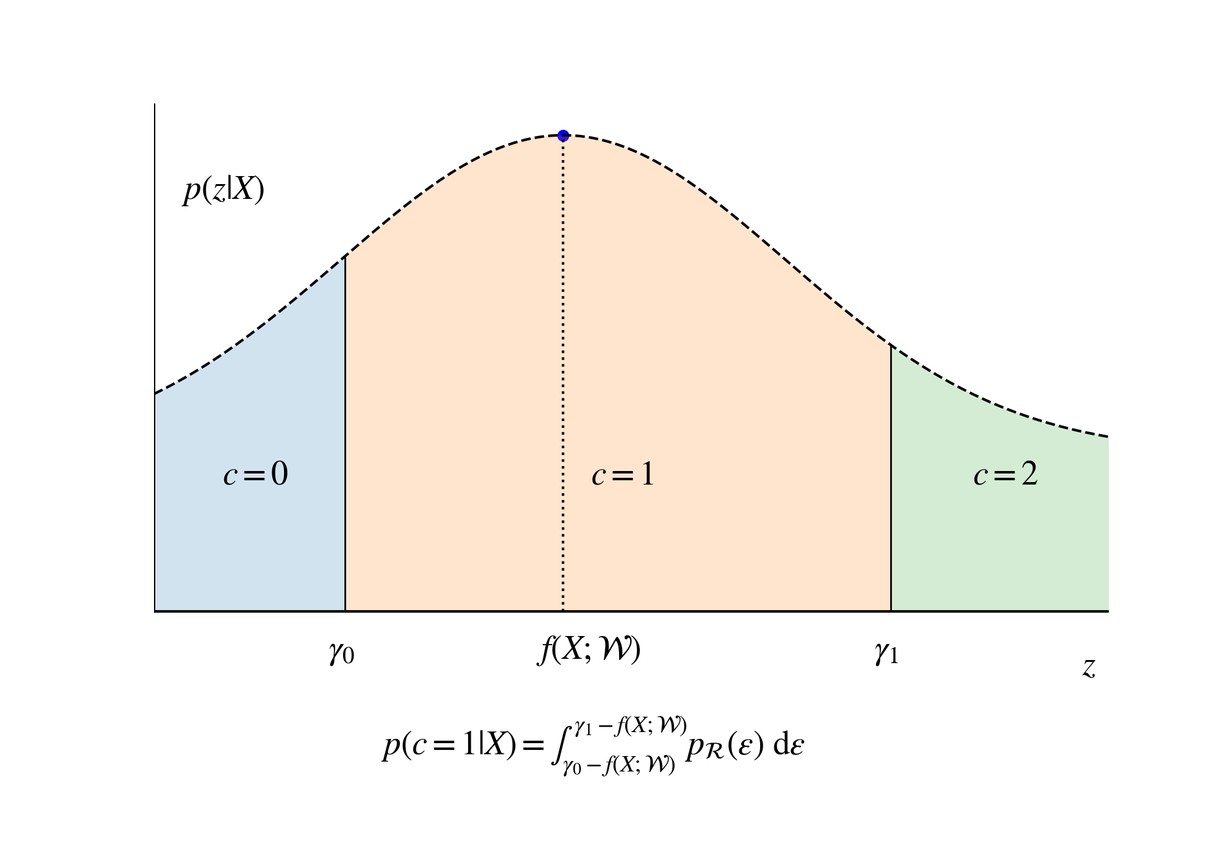
$z$から年収区分値は以下のルールで定まると仮定します (下図参照):
$$ c = \begin{cases} 0 & ( z < \gamma_0) \\ \ddots & \\ a & ( \gamma _{a-1} \le z < \gamma _a) \\ \ddots & \\ K - 1 & ( \gamma _{K-2} \le z) \end{cases} $$
ここで、新たなパラメータとして閾値の集合$ \left\{ \gamma _ i \right\} _{i=0} ^{K-2} $が導入されました。今回の場合、標語的には$\gamma _0 $ は「“年収500万円以下"と"500万円-600万円"の境界」、$\gamma _1 $ は「“500万円-600万円"と"600万円-750万円"の境界」などと考えることができます。
$\varepsilon$ についての周辺化を行うと、$\mathcal{R}$の累積分布関数 $F_{\mathcal{R}}$でもって
$$ p(c = C | X, \mathcal{W}, \gamma ) = \int _{ \gamma_{C-1} - f(X;\mathcal{W})} ^{\gamma_{C} - f(X;\mathcal{W})} d \varepsilon \mathcal{R}(\varepsilon) \nonumber \\ = F_{\mathcal{R}}(\gamma_{C} - f(X;\mathcal{W})) - F_{\mathcal{R}}(\gamma_{C-1} - f(X;\mathcal{W})) $$
と書けます。 $f$ が線形かつ $\mathcal{R}$ がロジスティック(正規)分布の場合このモデルは順序ロジット(プロビット)回帰モデルと呼ばれます。
パラメータ( $\mathcal{W}$と$\gamma $ )の推定は、
- 最尤法
- 変分推論
- MCMC
などで行うことができます。
Factorization Machineによる交互作用の導入
先ほど触れた通り、順序回帰は社会心理学における効果測定のような文脈で発展してきたという経緯があるためか(?)、通常は$ f(X; \mathcal{W})$ として線形なものを仮定します。今回は回帰係数の解釈が最終目的な訳ではなく、予測に興味があるのでもう少し複雑な関数系を仮定します。レジュメデータはテキスト以外にも様々なスパースな属性値を含んでいるため、今回は$f$としてFactorization Machine (FM) を考えることで、二次の交互作用の導入を目論見ます。すなわち、 $r$次元のベクトルの$D$個の集合であるパラメータ $\mathbf{v}$ を導入し、以下の関数形を考えます:
$$ f(x; w_0, w, \mathbf{v}) := w_0 + x \cdot w + \sum_{i < j } x_i x_j \mathbf{v}_i \cdot \mathbf{v}_j $$
低ランク構造のおかげで、FMでは交互作用を導入しても、パラメータの推定はそれほど高コストにならないという著しいメリットがあります。 推論も最尤推定や変分推論で効率よく行うことができますが、以前よりFMではギブスサンプリングによって予測事後分布を導出する方法が最も高い精度が出ることが知られていました。そこで、今回、順序プロビット限定(共役性のため)で、「俺のFactorization Machine」ことmyFMに、順序プロビットFactorization Machineを世界で初めて(多分)実装しました!おかげで誤差関数($\mathrm{erf}$)の漸近的な扱いに結構詳しくなれました。
給与推定の為に作った機能ですが、
- 心理学とかマーケティングで頻出の、順序尺度データに対する因子分析(欠損込み)
- Movielensのレーティングなど、本来連続値じゃなさそうな場合の回帰問題
などにも使えるはずですので、宣伝させていただきます。Movielens 10MのSOTAを若干更新することもできたので、興味のある方はレポジトリをご覧ください。
補間曲線による連続値のサンプリング
順序回帰のセッティングによって
「あなたのレジュメから推定される年収区分値は。。。 "750万円-1000万円"です!」
みたいな予測はできるようになるんですが、これだと数字のキリが良すぎて「すごいAI」感があまりでないですよね。。やっぱり区分値でなくて年収の値を予測して、かっこいい図をみたいのが人情かと思います。
今回の論文では、区分値データから連続値を回復する方法として、補間曲線を用いたサンプリング法を提案しました。
メインの仮定: $z$ と給与値の対応
心理学のデータ分析だと「大変そう思う」「そう思う」といった抽象的な尺度データを相手にする必要がありますが、今回給与の区分値データの場合は「実際の給与値」という現実に存在している(けれど観測できない)数値が背後に存在しています。そこで、$z$と実際の給与値$s$には、単調増加関数$g$によって
$$ s = g(z) $$
という対応関係が存在すると考えます。関数 $g$ は、ノイズが正規分布やロジスティック分布に従う「性質のよい空間」から給与が分布する「複雑な空間」へのマップの役割を果たしてくれます。さて、 $g$ の関数形は不明なのですが、連続性を仮定すれば閾値 $\left\{\gamma _i \right\}$ については $g$ の値が分かります。例えば $z < \gamma_0\ \to g(z) < \text{500万円}$, $z > \gamma_0\ \to g(z) > \text{500万円}$であるので、そもそも $ g(\gamma_0) = \text{500万円} $である必要が生じる為です。
テクニカルな仮定たち
こうして $g$ の値は数点の上では分かるのですが、もちろんこれらの点の上を通る曲線は無限にあり、内点での値を求めるには補間に頼る必要があります。幸いなことに$g$は単調なのでPCHIPなどによる補間は大変尤もらしく、ここからくる誤差は無視できそう(確実に突っ込まれる言葉遣い)でした。もっとベイジアンに徹するならば、単調増加制約付きのガウス過程とか、geometric brownian motion(の積分)とかを事前分布にするのだと思うのですが、力尽きたので今後の課題とします(この辺が好きな人、教えてください)
問題は $ z < \gamma0$ と $ z > \gamma _{K-2}$の外部領域でして、これらについては何らかの別の情報が必要となります。$ z < \gamma_0 $の場合は、「給与は負にならないので $ \lim{z\to -\infty} g(z) = 0$」という強い信念と、対数正規性という広く認められる現象から
$$ g(z) \sim C \exp(D z) $$
という仮定をおいて、$\gamma_{0}$での連続微分可能性を要求して$C$と$D$を決定する、という方針を採用しました。これも実際フィットしてみたら結果オーライ感はありました。 一方、 $z > \gamma_{K-2}$ はさらに難しく、ほぼノーヒントという状況です。ただ、
- そもそもこれは「年収5000万円以上」の領域に相当し、流石に対象となる方も多くはない
- どのみちノイズ$\varepsilon $ からの寄与が大きく、補間がちゃんとしていても目安程度のことしか言えないことが予想される
ので、こちらは$z < \gamma_{K-2}$の領域を単純に線形補間することで誤魔化す、という方針をとりました。
外挿はこのように技術的に難しいのですが、 $z$ 空間でみた時の予測事後分布の中央値 $z^{(\text{med})}$ は多くの方について $ \gamma*0 < z^{(\text{med})} < \gamma *{K-2} $ を満たしており、その場合年収空間での中央値 $ s^{(\text{med})} = g(z^{(\text{med})}) $ は(PCHIPによる)内挿にのみ依存するので、中央値を予測値と思えばある程度外挿に対してロバストな結果が得られます。
給与値サンプリングの手続き
上記の補間により、変分法やギブスサンプリングで$\mathcal{W}$と$\gamma$のサンプルを求めておけば、レジュメ$X$が与えられた時の給与値の予測事後分布から、以下の手続きによって値をサンプルすることができます:
- $\mathcal{W}$と$\left\{\gamma\right\}$をドロー
- $\left\{\gamma\right\}$の補間と外挿を行って、$g$を決定
- $\varepsilon \sim \mathcal{R}$をドローし、$z = f(X; \mathcal{W}) + \varepsilon $を計算
- $s = g(z) $をサンプルに加える
実験
以下、実際のビズリーチのデータでの実験結果について述べます。前提として、特徴量は
- 年齢や経験社数などの数値データをパーセンタイルで離散化+one-hot化したもの
- 所属企業・職種などのカテゴリ属性値を、ある程度頻度のあるもののみone-hot化
- 本文テキストをLDAでtopic化したもの(これには俺のLDAを使いました)
などで、5000次元ほどの行列となります。
結果1: 分類問題としての精度比較
まずは分類問題としての性能を測定したいと思います。主なresearch questionは
- 線形vs Factorization Machineで差が出るのか
- 推論方法は最尤推定vs変分推論(VI) vs Gibbsサンプリングで差が出るのか
の二点かと思います。
各アルゴリズムの実装は以下のものを用いました:
- 線形 + ロジット + 最尤推定にはmordを用いる。正則化係数は交差検証で決める。このライブラリは内部的にはL-BFGSを使っていました。
- 変分推論にはpymc3の自動微分変分推論でお手軽に行う(順序プロビットの場合は学習の安定のため、$\mathrm{erf}$の漸近系にかなり注意を払いました。ちゃんと考えると安定するのが楽しかったっす)。収束のために特段何かしなければならなかった、ということもなく、minibatchサイズ依存性も無視できるものでした。
- プロビット + GibbsサンプリングにはmyFMを用いる
FMの場合の次元数はいずれの場合も交差検証の結果32付近で最適でしたので、今回は全て32に統一します。
モデル、ノイズ分布、推論方法別の精度は以下のようになりました:
| model | Log-loss | Accuracy | MAE |
|---|---|---|---|
| 線形 + ロジット + 最尤推定 | 1.176 | 0.519 | 0.651 |
| 線形 + ロジット + 変分推論 | 1.176 | 0.519 | 0.655 |
| 線形 + プロビット + 変分推論 | 1.194 | 0.515 | 0.670 |
| 線形 + プロビット + Gibbsサンプリング | 1.193 | 0.517 | 0.673 |
| FM + ロジット + 変分推論 | 1.156 | 0.525 | 0.639 |
| FM + プロビット + 変分推論 | 1.179 | 0.521 | 0.662 |
| FM + プロビット + Gibbsサンプリング | 1.158 | 0.530 | 0.638 |
- FMに依る相互作用の導入で、確かに性能は向上する
- 推論方法をVIに固定した場合は、ロジスティックノイズの方が高性能である
- ノイズを正規分布に固定した場合は、FMではGibbsサンプリングの方が勝っている
ということがみて取れると思います。ロジット + VI vsプロビット + Gibbsは伯仲していますが、ちょうどロジスティックの場合のアドバンテージとGibbsサンプリングのそれとが釣り合う感じですね。悩みます。
線形かつロジスティックの場合に変分推論と最尤推定では性能にほぼ差がないですが、変分推論は交差検証せずに(hyperpriorを正則化係数に与えれば)ちゃんと精度が出ていて、パラメータチューニングも含めた実行時間的にはむしろ変分推論の方が有利でした。
また、LDAのtopic分布で小さい値のところを0にして疎性を半ば強引に上げると、myFMでmordの最尤推定に速度で完勝できて嬉しうございました。
FMとか線形回帰の係数たちには世の中の真実が隠されていましたが、とてもお見せできそうにないです…
結果2: Factorization Machineのスコアvs年収の関係
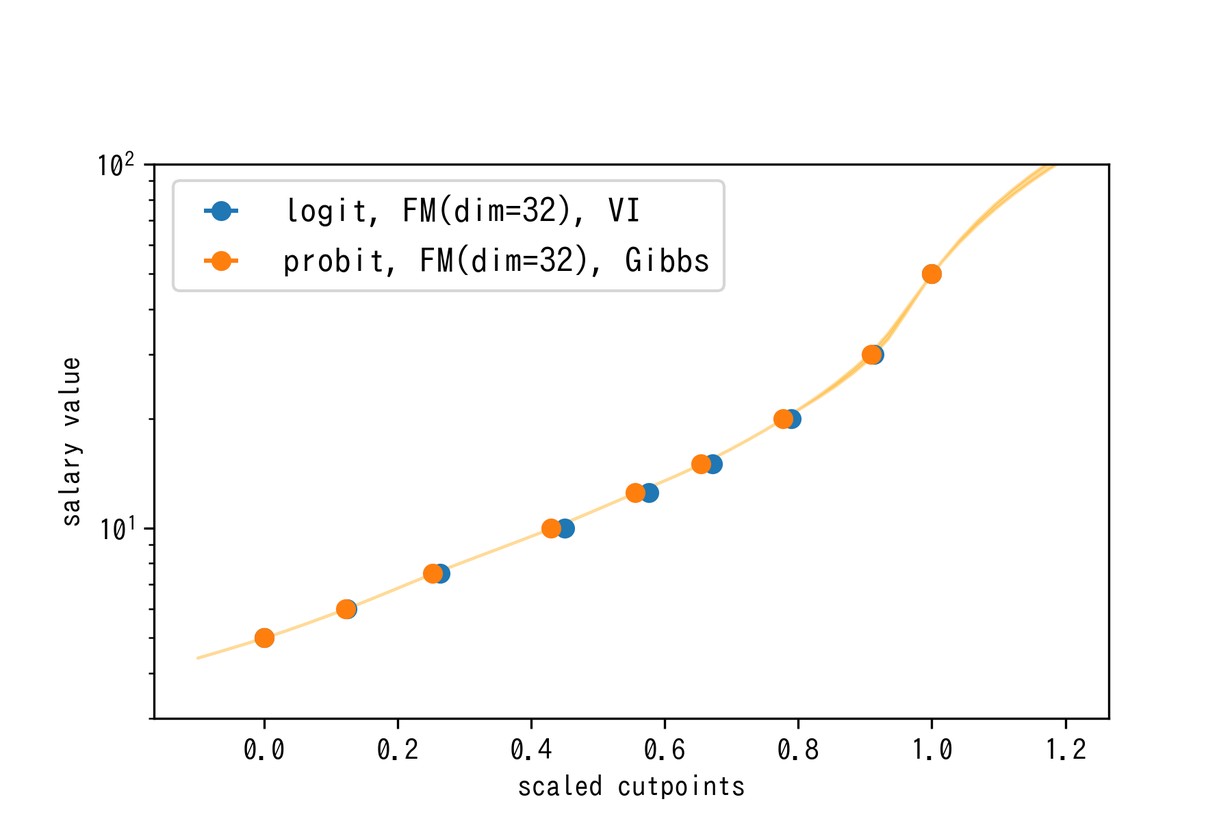
連続サンプル値を得てみる前に、閾値$\left\{ \gamma _i \right\}$と実際の金額の境界線をプロットしてみましょう。結果は以下のようになります:
縦軸はログスケールになっており、直線になっていそうな部分ではFMのスコアと実際の年収値に指数関数的な関係が存在することが示唆されます。仮にFMのスコア分布が正規分布でノイズも正規なのであれば、対数正規性は妥当な仮定なのだと思われます。
高年収側に進むにつれて指数関数よりさらに強い関数で年収が上昇していく、という事も分かります。ハイクラスになってくると、ノイズも含めたちょっとの差が大きく年収を変えるわけですね(ということで、みなさん良い転職をして頂ければと思います)。この図によると「レジュメ的には年収600万円の方がノイズによって500万円以下になってしまう確率」と、「年収5000万円の方がノイズで3000万円以下になってしまう確率」って同程度(むしろ後者の方が高い)というのはなかなか衝撃的ですね。
結果3: 事後サンプルの抽出結果
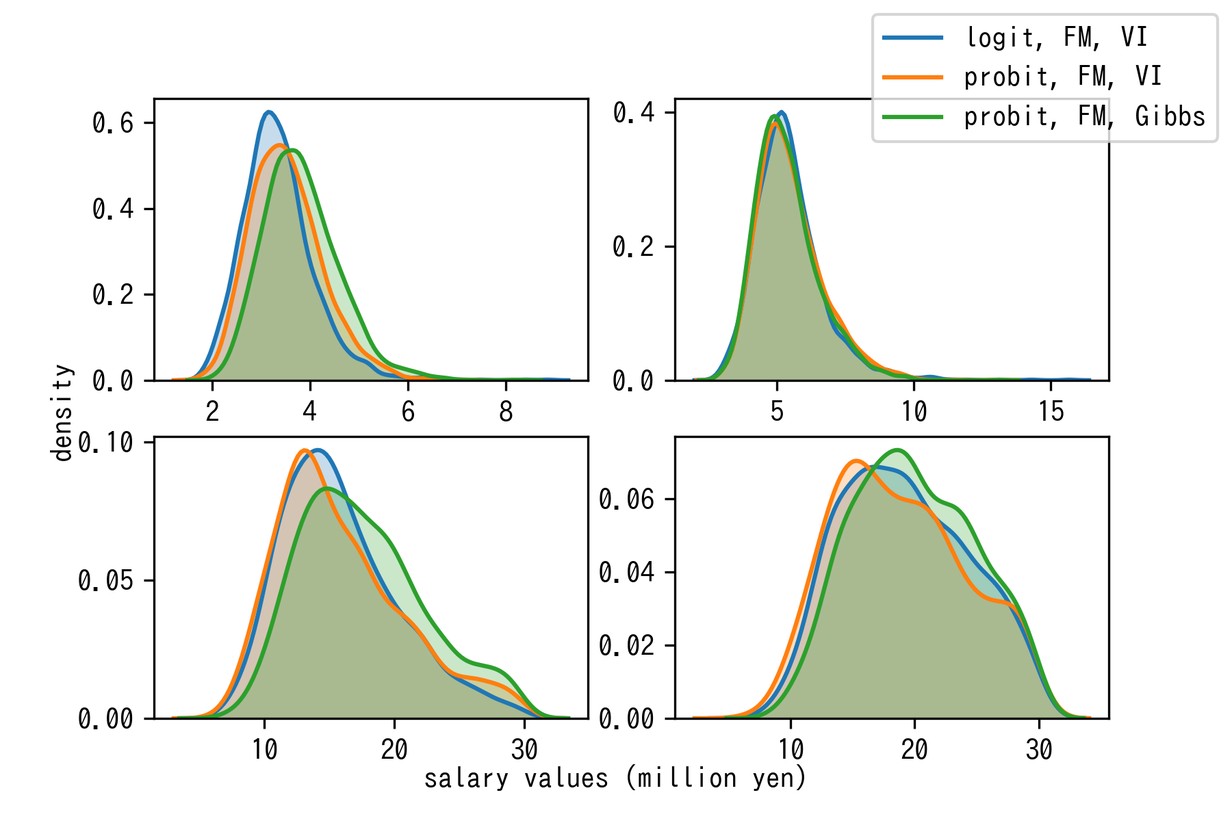
内点の単調補間 + 外挿という上記の提案手法で可能になった予測事後分布を実際のユーザーデータに適用すると、以下のような密度推定が得られました:
推論方法やノイズ分布に依らずに概ね同じ結果に収束していそうで安心しました。 上二段では勝手に対数正規分布のような事後分布になっているのもそれっぽいですね。ロジスティックノイズの方が裾を引かないように見えるのが一見不思議ですが、これは閾値間の幅が広く推定されることで辻褄が合っています。
グループ内では「頑張ったのは分かるんですが、そもそも対数正規性仮定した上で、区分値の中からlog-uniformに教師値をサンプリングしてくるっていうアプローチと結果違うんですか〜?」という大変鋭い指摘をもらって、最初はうっとなったんですが、下二段はパラメータの不確かさ + 補完曲線のsuper-exponentialな振る舞いが合わさって対数正規らしからぬ分布が出現していると思われるので、意味はあるんやでと言いたいところです。
おわりに
今回は特に順序プロビット + Factorization Machineの開発というところを結構頑張ったのですが、しかし順序ロジット + 変分推論に勝てたとは言い難い結果でした。給与に効くノイズとしては正規分布よりロジスティック分布の方が適切だ、という事なのかもしれないですね。まぁ実装は楽しかったし今後他の用途でも使えそうなので満足です。いつもマニアックなことに時間を使わせてくれるAIグループの皆様に感謝。